Articulations
Introduction
Articulations provide an alternative, often superior approach to simulating mechanisms over adding joints to rigid bodies. Typically, we achieve higher simulation fidelity with articulations as they have zero joint error by design, and can handle larger mass ratios between the jointed bodies. PhysX simulates articulations in reduced-coordinates, where the configuration of the articulation is determined by its root-body pose and the joint angles instead of the world pose of each body involved.
It is often possible to turn jointed rigid bodies into an articulation given that they do not contain unsupported joints, see Articulation Joints below, and making sure that loops are resolved appropriately.
Besides e.g. ragdoll simulation in games, articulations are suitable for robotics and other applications that require accurate simulation of mechanical structures. They further provide specialized features for mechanisms and robotics such as:
Fixed Tendons that can create constraints on joint angles, for example to enforce mirrored motion of two joints, or
Spatial Tendons that can create distance constraints between attachment points on articulation links, or
Articulation Tree structure
Articulations must have a tree structure in terms of their links and the joints between them (closing loops is possible, however). Consider these two example articulations: A ragdoll and a robotic arm.

The tree structure for the arm is straightforward: The root is at the base on the ground plane, and revolute joints connect the different links up to the manipulator, where the tree has its only branch to connect the two gripper parts to the arm through prismatic (i.e. linear) joints.
The ragdoll also has a tree structure: For example, we can choose the head to be the root, and connect the torso to it with a spherical joint, which in turn uses spherical joints to attach the arms, and so on. The tree structure would be broken if the ragdoll was handcuffed such that the hands, arms, and torso form a loop.
Floating and Fixed-Base
There is a difference between the two articulation examples: The ragdoll is a floating articulation which means the root (e.g. the head) may move freely in space.
The robot arm is a fixed-base articulation: Its root or base is fixed to the world frame. The fixed-base property can be set with a flag on the articulation at creation. Setting this flag is advantageous over constraining the root link using a Fixed Joint because the immoveable property of the root link is solved perfectly.
Closing Loops
While articulations natively only support tree-structures, it is possible to create loops in the articulation by adding rigid-body Joints between articulation links. For example, we could tie the ragdoll’s hands together by adding a Distance Joint between the two hand spheres.
Reduced-Coordinates and Comparison to Rigid Bodies
The links that make up an articulation are actors like rigid bodies, but they are simulated as a unit. One of the differences between a link and a rigid body is that it is not possible to set a link’s global pose or velocity directly. This is due to the reduced-coordinate representation: The pose of a link is determined recursively through the pose of its parent link and the position of the joint connecting it to the parent (velocities are analogous). For the same reason, links cannot be kinematic. You may find more details about reduced coordinates below.
The articulation links also do not have individual sleep states or solver iteration counts because they are simulated as a unit in the articulation. Those properties are set on the articulation instead. For the same reason, the links do not support force thresholding.
Otherwise, articulation links can be treated as rigid bodies; for example, they use the same mass and collision-shape setup API, or we can apply a spatial force to them, or we can query their world pose and velocity (querying is ok, setting is not). In particular, links are also compatible with rigid-body Joints that can be used to close loops.
Performance-wise, the simulation cost is generally proportional to the number of degrees of freedom, rather than the number of links (assuming few contacts that need resolving). Therefore, in common robotics applications, where most joints have 0-1 degrees of freedom, the simulation cost of reduced-coordinate articulations is often lower than using rigid-bodies with joints.
Creating an Articulation
First, create the articulation actor without links:
PxArticulationReducedCoordinate* articulation = physics.createArticulationReducedCoordinate();
Set the articulation to be fixed-base, if applicable, and any other optional configuration options (see the API doc of PxArticulationFlag and PxArticulationReducedCoordinate for more information):
articulation->setArticulationFlag(PxArticulationFlag::eFIX_BASE, true);
articulation->setSolverIterationCounts(minPositionIterations, minVelocityIterations);
articulation->setMaxCOMLinearVelocity(maxCOMLinearVelocity);
// etc.
Then add links one by one, each time specifying a parent link (NULL for the parent of the initial link), and the pose of the new link:
PxArticulationLink* link = articulation->createLink(parent, PxTransform(PxIdentity));
PxRigidActorExt::createExclusiveShape(*link, linkGeometry, material);
PxRigidBodyExt::updateMassAndInertia(*link, 1.0f);
Note that the initial poses of the child links may be set to arbitrary transforms since the child link poses are computed from the base link pose and the joint positions when they are set to their initial values via the cache, see PxArticulationCache. Hence one can just pass an identity PxTransform.
Each time a link is created beyond the first, a PxArticulationJoint is created between it and its parent. Specify the joint frames for each joint, in exactly the same way as for a rigid-body PxJoint:
PxArticulationJointReducedCoordinate* joint = link->getInboundJoint();
joint->setParentPose(parentAttachment);
joint->setChildPose(childAttachment);
and configure the joint type and motion - here an example of a joint with a limited motion range:
joint->setJointType(PxArticulationJointType::eREVOLUTE);
// revolute joint that rotates about the z axis (eSWING2) of the joint frames
joint->setMotion(PxArticulationAxis::eSWING2, PxArticulationMotion::eLIMITED);
PxArticulationLimit limits;
limits.low = -PxPiDivFour; // in rad for a rotational motion
limits.high = PxPiDivFour;
joint->setLimitParams(PxArticulationAxis::eSWING2, limits);
Note how the axis must be specified consistently for both setting the motion and limit. In addition to limits, you may add a joint drive (i.e. motor):
PxArticulationDrive posDrive;
posDrive.stiffness = driveStiffness; // the spring constant driving the joint to a target position
posDrive.damping = driveDamping; // the damping coefficient driving the joint to a target velocity
posDrive.maxForce = actuatorLimit; // force limit for the drive
posDrive.driveType = PxArticulationDriveType::eFORCE; // make the drive output be a force/torque (default)
// apply and set targets (note again the consistent axis)
joint->setDriveParams(PxArticulationAxis::eSWING2, posDrive);
joint->setDriveVelocity(PxArticulationAxis::eSWING2, 0.0f);
joint->setDriveTarget(PxArticulationAxis::eSWING2, targetPosition);
You may also set joint friction, armature, etc; see the API doc of PxArticulationJointReducedCoordinate for details. At creation, you can also add Articulation Tendons:
PxArticulationFixedTendon* fixedTendon = articulation->createFixedTendon();
// setup tendon
Finally, add the articulation to the scene (see caveat below about changing articulation topology after scene insertion):
scene.addArticulation(*articulation);
Changing the Topology of an Articulation that is in a Scene
In order to allow for pre-computing and optimization of simulation data, it is not possible to make changes to an articulation that change its topology after the articulation has been added to the scene. Topological changes include:
If you need to make topology changes, simply remove and re-add the articulation to the scene:
scene->removeArticulation(*articulation);
// make topology changes
scene->addArticulation(*articulation);
The articulation state (i.e. pose and velocities) is preserved through the remove and re-add cycle, so you do not have to store and reapply the state. In case of link removal, the corresponding joint state is removed as well; the state of joints of new links may be set with PxArticulationJointReducedCoordinate::setJointPosition() and PxArticulationJointReducedCoordinate::setJointVelocity() or the PxArticulationCache. Note that any changes to the articulation topology, in particular changes affecting degrees-of-freedom, typically require recreating the articulation’s PxArticulationCache and recomputing low-level indices to the cache.
Articulations and Sleeping
Like rigid dynamic objects, articulations are put into a sleep state if their energy falls below a certain threshold for a period of time. In general, all the points in the section Sleeping apply to articulations as well. In particular, articulations can only go to sleep if each individual articulation link fulfills the sleep criteria, analogous to jointed rigid-bodies.
Articulation Joints
The PxArticulationJointReducedCoordinate provides an interface that is similar to the PxD6Joint interface for rigid-body joints. However, it incurs certain limitations. By default, all axes are locked and the joint type is undefined. The joint types are:
PxArticulationJointType::eFIX- a fixed joint with zero degrees of freedom (DOF)PxArticulationJointType::ePRISMATIC- a prismatic (sliding) joint with one DOFPxArticulationJointType::eREVOLUTE- a revolute (hinge) joint with one DOF whose position is automatically wrapped at +/- 2pi.PxArticulationJointType::eREVOLUTE_UNWRAPPED- same as a revolute, but without position wrappingPxArticulationJointType::eSPHERICAL- a spherical (ball-in-socket) joint with two to three DOFs
See Creating an Articulation for setup example code.
Articulation joints are not breakable like rigid-body joints. Furthermore, note that spherical joints are a special case: while it is technically possible to configure a spherical joint to only have one DOF, you should use a revolute joint instead for performance. When there are two or more degrees of freedom unlocked, rotational motion is integrated by rotating by decomposed quaternions rather than by Euler angles to avoid gimbal lock. However, this technique can lead to rotational axis drift, which is corrected by additional constraints in the simulation, which could lead to slight movement on the remaining locked rotational axis.
Articulation Joint Drives
In addition, a drive may be added to a joint. As with limits, this is defined on a per-axis basis. The drives operate analogous to a PD controller (see implementation note below) and have two terms: stiffness and damping. Stiffness controls how strongly the drive drives towards a target joint position/angle and damping controls how strongly the joint drives towards a target velocity. Let’s consider again the sample setup code in Creating an Articulation:
PxArticulationDrive posDrive;
posDrive.stiffness = driveStiffness; // the spring constant driving the joint to a target position
posDrive.damping = driveDamping; // the damping coefficient driving the joint to a target velocity
posDrive.maxForce = actuatorLimit; // force limit for the drive
posDrive.driveType = PxArticulationDriveType::eFORCE; // make the drive output be a force/torque (default)
// apply and set targets (note again the consistent axis)
joint->setDriveParams(PxArticulationAxis::eSWING2, posDrive);
joint->setDriveVelocity(PxArticulationAxis::eSWING2, targetVelocity);
joint->setDriveTarget(PxArticulationAxis::eSWING2, targetPosition);
With these parameters, the joint drive pushes the joint position towards targetPosition [rad] and the joint velocity toward targetVelocity [rad/s]. Assuming that the scene units are (SI) meters, the drive output is a torque in [Nm], the driveStiffness gain on position is in [Nm/rad], and the driveDamping gain on velocity is in [Nm/(rad/s)].
If the driveType is instead set to PxArticulationDriveType::eACCELERATION, the drive output is a joint acceleration, which can be useful to obtain behavior that is independent of the mass and inertia of the links. For an acceleration drive, the driveStiffness gain has units [rad/s^2 / rad], and driveDamping is in [rad/s^2 / (rad/s)].
An key articulation flag related to drives is PxArticulationFlag::eDRIVE_LIMITS_ARE_FORCES: If it is set, the forceLimit above refers to a force/torque (e.g. N and Nm), and, otherwise, to an impulse (force * dt, or torque * dt). The limit applies to both force- and acceleration-type drives.
The joint drive can be made into a velocity drive tracking targetVelocity by setting driveStiffness to zero and an appropriately tuned driveDamping. By default, the target velocity of the drive is set to 0 [rad/s], so a nonzero damping parameter results in the drive being an PD controller where the P gain, i.e. the stiffness, acts on the position error and the D gain, i.e. the damping, acts on the derivative of the position error, i.e. opposing the joint velocity.
Note
An important implementation detail is that the drives are implicit, i.e. the position and velocity constraints imposed by the drive that the solver iterates on are with respect to the end of the time step, and not, as usual in engineering, implemented as an explicit, constant-during-time-step drive force calculated from the gains and the joint position and velocity at the beginning of the time step. A key advantage of the implicit formulation is that it can handle very large gains without necessarily causing joint state instability or oscillations. This holds true for drives in isolation but does not necessarily hold true for very stiff drives in conjunction with other hard constraints such as mimic joints, joint position limits or joint velocity limits. This is discussed in more detail in Section Articulation Drive Stability. For low gains and sufficiently small time steps, the implicit and explicit drive dynamics are practically identical. This is discussed in more detail in the accompanying document
Implicit Spring Joint Drives.The articulation cache dof constraint force flag
PxArticulationCacheFlag::eJOINT_SOLVER_FORCEShas been deprecated. The reported forces are incorrect. Please use thePxArticulationCacheFlag::eLINK_INCOMING_JOINT_FORCEcache member instead, see Link Incoming Joint Force.
Articulation Drive Stability
The accompanying document Implicit Spring Joint Drives describes the implicit drive model implemented by PhysX. A key advantage of the implicit formulation is that it is generally more stable with very large gains. This holds true for joint drives in isolation. When joint drives are coupled with other hard constraints such as contacts, mimic joints or joint limits, however, the outcome is not necessarily stable. Moreover, there is no guarantee that all constraints are satisfied or even approximately satisfied. This section describes the difficulties that arise when the drive force is so large that it leads to effectively kinematic drive; that is, a drive that is resolved in a single step.
A simple example that demonstrates a system of constraints that is hard to resolve is a finger pressing downwards on a box. This is illustrated in Figure A simplified articulated finger.
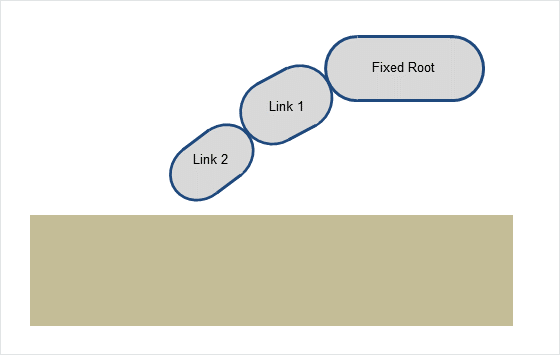
A simplified articulated finger
The three links depicted in Figure A simplified articulated finger illustrate a simplified finger. The joint coupling the fixed root link and Link 1 represents the finger’s proximal joint, while the joint coupling Link 1 and Link 2 represents the finger’s distal joint. In this example, both joints are revolute with a single degree of freedom permitting the two dynamic links to rotate downwards towards the static box. A positive joint angle applied to the proximal joint will move both links closer to the box. A positive joint angle applied to the distal joint will move Link 2 closer to the box. The proximal joint is driven to a large positive angle way beyond the value that brings the fingertip into contact with the box. The drive is sufficiently stiff that, in the absence of the static box, the drive target would be achieved in less than a single timestep. The distal joint, meanwhile, is configured with a joint limit that prevents negative joint angles. This configuration results in three competing constraints: drive, joint limit and contact.
PhysX employs an iterative Gauss-Seidel solver to resolve coupled systems of constraints. The outcome of each constraint resolution is a modification of the joint and associated link speeds. The solver performs a number of iterations in which the constraints of each articulation are resolved sequentially in isolation. Within a single articulation, the algorithm traverses outwards from root to tip and solves all constraints for each link and its corresponding inbound joint in the order that the links and inbound joints are encountered. This requires a specific ordering for the constraints of a single link and its corresponding inbound joint. The sequence is as follows:
Constraint Sequence |
|---|
Link Dynamic Constraint |
Link Dynamic Contact |
Mimic Joint |
Joint Drive |
Joint Position Limit |
Joint Velocity Limit |
Link static constraint |
Link static contact |
The key takeaway from the articulation constraint sequence with regard to the finger model is the ordering of joint drive, joint position limit and link static contact. At the moment of contact, the stiffness of the proximal joint drive is sufficiently large to produce a joint velocity that would achieve the target angle in a single solver iteration. After resolving the drive, Link 1 has a positive angular velocity that is rotating downwards towards the static box. Link 2, meanwhile, follows Link 1 so that the finger remains straight. Another way of expressing this is that the distal joint remains at a joint angle of zero and a joint velocity of zero. The lower limit of the distal joint is not yet breached and has no impact on the system state. Finally, the contact produces an impulse that will produce a negative angular velocity on Link 2 and a negative distal joint velocity. In the absence of further solver iterations, the limit of the distal joint will be breached when the joint positions are forward integrated with the most recent velocities generated by the solver.
As already discussed, PhysX runs the solver over multiple iterations per simulation step. On the 2nd iteration, the strong drive of the proximal joint produces pretty much the same joint speed as on the 1st iteration. The difference now is that the limit of the distal joint recognises that the current joint velocity will breach the limit. It will attempt to straighten the finger by applying an impulse that will have a positive impact on the joint velocity of the distal joint. Link 1, however, will still have a large and positive angular velocity from the proximal joint drive. If it had a negative angular velocity it would be able to lift the fingertip out of contact but this is not the case. The contact impulse therefore will once again trigger and create a system velocity that will breach the limit of the distal joint when the joint positions are forward integrated.
On subsequent iterations, the pattern of drive, limit and contact repeats itself. The hope is that subsequent iterations will find an equilibrium that balances the relative strengths of drive, limit and impulse. This cannot happen if nothing yields. Drive, limit and contact all behave as hard constraints, each overwriting the effect of the last in roughly the same way across all iterations: adding more iterations will make no qualitative difference to the outcome. Moreover, the constraint that runs last will ”win” because the joint velocities arising from the impulses of that final constraint will be used to forward integrate the joint positions. In this case, the final impulse arises from static contact and produces a distal joint speed that will violate the distal joint limit. The outcome is depicted in Figure A simplified articulated finger with broken distal joint limit.
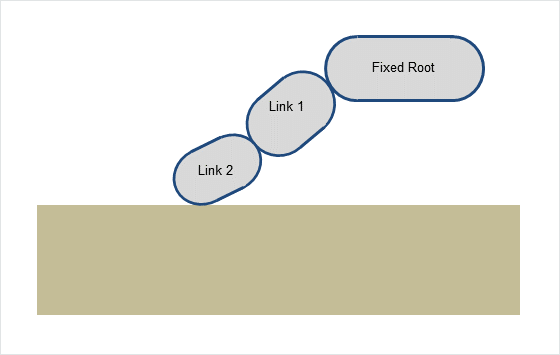
A simplified articulated finger with broken distal joint limit
Figure A simplified articulated finger with broken distal joint limit illustrates the broken distal joint limit. The broken joint limit is a consequence of a system of constraints in which nothing yields. Each iteration repeats the pattern of the last so that the solver cannot proceed towards a solution that represents a balance of forces. Any system that follows this template will be difficult to resolve and will result in either instability or obviously broken constraints.
Another example might be a short chain with three links and a fixed base. If one of the joints is driven with a very stiff drive and the other driven by a mimic joint set up to track the drive, this will take many solver iterations to resolve. The drive continually drives one of the joints to a target joint speed. The mimic joint then applies a negative impulse to one joint and a positive impulse to the other to ensure that both joints have the same speed. The mimic joint therefore overwrites the outcome of the joint drive and the drive overwrites the outcome of the mimic jont. This process repeats over many iterations with little scope for either constraint to yield to the other. Many iterations will be required to resolve both constraints. When this is combined with other hard constraints, such as limit and contact, the solver has an increasingly hard time to find a balance between all of the constraints.
The solution to the issues described above is to reduce the stiffness in the system. This is typically achieved by reducing the drive stiffness, damping and maximum force or by reducing the timestep to ensure that the drive target is not achieved in a single solver step or simulation step. It still remains the case, however, that it might not be possible to resolve all constraints simultaneously. For example, if a joint drive results in a joint speed that exceeds the joint’s speed and position limits it might not be possible to resolve both speed and position limit due to the constraint ordering. The key point here is that the constraint resolved last in the sequence overwrites the outcome of the previous constraints. In this case, the outcome of resolving the joint speed limit might be counter to the outcome of resolving the joint position limit.
Joint Positions and Velocities
Reduced-coordinate articulations internally keep track of scalar joint positions, velocities, and accelerations, with one entry corresponding to each degree of freedom (DOF). Joint position represents the relative offset between a parent and child link, and their corresponding joint frames in particular, along/around a DOF. If it is a rotational axis, the joint position represents an angle in radians. If it is a translational axis, the joint position represents a distance in whatever units the simulation is being performed in. Similarly, joint velocities are in radians/s or distance/s, for a rotational and linear DOF.
The joint positions determine the links’ poses: The root link’s world space pose provides a reference frame from which the poses for all other links in the articulation are calculated from the joint positions. This ensures that there cannot be any joint separation or offsets in locked axes.
The caveat with this approach is that it is not possible to directly update the pose of links in an articulation because this new transform could violate locked axes or could differ from the joint position. Instead, it is necessary to update the joint positions, which triggers new link poses to be computed. This ensures that the internal data from which poses are computed is consistent at all times. See PxArticulationCache below for more information on how to set/read joint positions and other internal data of the articulations.
Link velocities and joint velocities share a similar relationship. A link’s world-space velocity is derived from the world-space velocity of its parent link and the current joint velocity. This means that the root link stores a world-space velocity and all other links’ velocities are computed by propagating this velocity and the respective joint velocities through the articulation. As such, it is not possible to directly set the velocity of links in an articulation. Instead, it is necessary to modify the root and joint velocities from which the links’ velocities are calculated. It is legal to apply world-space forces on links. These will be propagated through the articulation as part of forward dynamics.
Note
Just like rigid bodies, all queries regarding link velocity and acceleration report the respective quantities in the world frame and with the links’ center of mass as reference point (and not the actor frame’s origin). However, also like rigid bodies, pose is reported with respect to the actor frame.
Reduced-coordinate articulation textbooks, e.g. Rigid Body Dynamics Algorithms by Roy Featherstone, use spatial accelerations to describe the rigid-body, i.e. link accelerations. PhysX does not report spatial accelerations, but classical, i.e. body-fixed accelerations.
Articulation Joint Friction
Joint friction is added to an articulation joint when a non-zero joint friction coefficient is used. The model used for articulation joint friction is equivalent to Coulomb friction. More specifically, the impulse required to bring a joint degree of freedom to rest, given its current velocity, is compared to the available friction impulse, that is, the magnitude of the forces acting on the joint multiplied by the joint friction coefficient. If there is enough available friction impulse to bring the joint degree of freedom to rest, then the joint is held at rest on this axis. Otherwise, all the available friction impulse is applied to the joint degree of freedom to slow it down.
The user can therefore customize the behavior of the articulation joint friction by changing the value of the friction coefficient (default value of 0.05).
Its value can be retrieved with PxArticulationJointReducedCoordinate::getFrictionCoefficient() and set with PxArticulationJointReducedCoordinate::setFrictionCoefficient().
The same value for the joint friction coefficient is used for all axes of a given joint.
Note
The joint friction may behave differently with
PxSolverType::ePGSandPxSolverType::eTGS. This is because the two solvers treat the accumulation of friction impulses throughout the subiterations differently. In particular, joint friction may appear weaker forPxSolverType::eTGSthan forPxSolverType::ePGS.
PxArticulationCache
Direct access to joint positions, velocities and forces, and other internal data that controls a reduced-coordinate articulation is provided through the PxArticulationCache class and the corresponding API in PxArticulationReducedCoordinate.
Create a cache as follows after you inserted the articulation into a scene:
PxArticulationCache* cache = articulation->createCache();
The cache is constructed specifically for the articulation and contains the exact memory needed to store data about that articulation. It cannot be shared between different articulations unless they have the exact same structure. Similarly, if the properties of an articulation change (e.g. a link is added/removed, or degrees of freedom are changed), it is necessary to release the cache and recreate it.
Once a cache has been created, it may be used to read articulation data by copying the data into the cache. In this case, all data is copied to the cache, but the copy may be filtered to data of interest with PxArticulationCacheFlag:
articulation->copyInternalStateToCache(*cache, PxArticulationCacheFlag::eALL);
Since the data in the cache is a copy of the articulation data, any modifications to the cache data do not alter the internal state of the articulation that copied the data to the cache. In order to update the internal state of the articulation, it is necessary to apply the cache, i.e. copy the data back to the articulation. In this example, we apply, i.e. copy just the joint positions:
articulation->applyCache(*cache, PxArticulationCacheFlag::ePOSITION);
Note that this will cause the link poses to be updated based on the newly set joint positions, and it is not legal to copy to or apply a cache while the simulation is running.
A cache stores sufficient information to be able to record the state of an entire articulation at a snapshot in time and then reset the articulation back to that state. It is legal to create and maintain multiple articulation caches for a given articulation.
A cache further provides access to the root link’s state, including transform, velocities and accelerations. See PxArticulationCache for further articulation data that may be accessed via cache.
Simple operations like zeroing the joint velocities can be done with the following code snippet:
PxMemZero(cache->jointVelocity, sizeof(PxReal) * articulation->getDofs());
articulation->applyCache(*cache, PxArticulationCacheFlag::eVELOCITY);
In addition to setting joint positions and velocities, it is possible to interact with the articulation through the application of joint forces/torques, which behave like an actuator, or by applying external forces to the links directly.
Cache Indexing
The data in the cache is stored in a specific internal low-level order that facilitates propagation through the articulation. The order imposed by the low-level indices may be different from the order in which the links and joints were originally added to the articulation. Therefore, the user must:
use a link’s low-level index
PxArticulationLink::getLinkIndex()for link-data indexing, e.g.PxArticulationCache::externalForces;calculate the low-level degree-of-freedom (DOF) data indices by summing the joint DOFs in the order of the links’ low-level indices:
Low-level link index: | link 0 | link 1 | link 2 | link 3 | ... | <- PxArticulationLink::getLinkIndex() Link inbound joint DOF: | 0 | 1 | 2 | 1 | ... | <- PxArticulationLink::getInboundJointDof() Low-level DOF index: | - | 0 | 1, 2 | 3 | ... |
The root link always has low-level index 0 and always has zero inbound joint DOFs. The link DOF indexing follows the order in PxArticulationAxis::Enum. For example, assume that low-level link 2 has an inbound spherical joint with two DOFs: eSWING1 and eSWING2 (and, in particular, eTWIST is locked with PxArticulationMotion::eLOCKED). The corresponding low-level joint DOF indices are therefore 1 for eSWING1 and 2 for eSWING2.
Snippet: Calculate the low-level DOF indices for an articulation:
const PxU32 nbLinks = art->getNbLinks();
std::vector<PxArticulationLink*> links(nbLinks, nullptr);
// The links vector is in the order that the links are added to the articulation using createLink.
// However, the index in links[index] and the low-level index links[index].getLinkIndex() may differ
// depending on the articulation.
art->getLinks(links.data(), nbLinks, 0);
std::vector<PxU32> dofStarts(nbLinks, 0);
dofStarts[0] = 0; // The root link never has an incoming articulation joint
// Put DOF counts into dofStarts in low-level index order
for(PxU32 i = 1; i < nbLinks; ++i)
{
PxU32 lowLevelIndex = links[i]->getLinkIndex();
PxU32 dofs = links[i]->getInboundJointDof();
dofStarts[lowLevelIndex] = dofs;
}
// Calculate DOF index offsets per low-level link index:
PxU32 count = 0;
for(PxU32 i = 1; i < nbLinks; ++i)
{
PxU32 dofs = dofStarts[i];
dofStarts[i] = count;
count += dofs;
}
Consider again the spherical joint described above and that it is the incoming joint of PxArticulationLink* link. We can set the position of the joint’s eSWING2 DOF with:
PxU32 jointSwingTwoIndex = 1;
cache->jointPosition[dofStarts[link->getLinkIndex()] + jointSwingTwoIndex] = newJointPosition;
In addition to reading and writing joint DOF data, the cache is used to read and write data for computations that can be performed using reduced coordinate articulations, for example, inverse dynamics and Jacobian matrix computations.
Articulation Tendons
Tendons create constraints within articulations. There are two types: Fixed and Spatial.
Fixed Tendons
Fixed tendons impose constraints on joint positions. For example, a fixed tendon can be setup such that it imposes an equality constraint between a driven and a passive revolute joint. More details are available in the API documentation for PxArticulationFixedTendon.
Spatial Tendons
Spatial tendons impose distance constraints between attachment points on links. This allows, for example, modeling hydraulic actuators that can push and pull on links, artificial muscles in a biomimetic robot, or elastic-string-like mechanical components. More details are available in the API documentation for PxArticulationSpatialTendon.
Mimic Joints
Mimic joints attempt to enforce a linear relationship between the positions of two degrees of freedom (dofs) of the same articulation instance. Each dof may be in any sub-tree of the articulation and the dof pair may be any combination of linear and angular type. An articulation may have multiple mimic joints applied and there is no restriction on the number of mimic joints referenced by any individual joint. The only restriction is that each dof of a mimic joint must be capable of motion (PxArticulationMotion::eFREE or PxArticulationMotion::eLIMITED).
Mimic joints are characterised by a gear ratio \(G\) and an offset \(\gamma\) such that:
with \(q_A\) and \(q_B\) denoting the positions of the two dofs coupled by the mimic joint.
PhysX mimic joints are implemented as two-way interactions that may apply unlimited impulses to the associated dofs in order to resolve the corresponding constraint equation. A full description of the mathematics of a PhysX mimic joint is provided in the accompanying document Mimic Joint Maths.
Mimic joints may be used to create a diverse range of joints such as rack-and-pinion joints, grippers and geared joints. Combinations of mimic joints may be used to create more complex joint types such as differential joints.
A mimic joint instance is created with the function:
PxArticulationMimicJoint* PxArticulationReducedCoordinate::createMimicJoint(const PxArticulationJointReducedCoordinate& jointA, PxArticulationAxis::Enum axisA, const PxArticulationJointReducedCoordinate& jointB, PxArticulationAxis::Enum axisB, PxReal gearRatio, PxReal offset, PxReal naturalFrequency, PxReal dampingRatio);
The combination of jointA and axisA specifies a single dof of the articulation. Similarly, jointB and axisB together specify the complementary dof of the mimic joint. The variables gearRatio and offset respectively play the role of \(G\) and \(\gamma\) in the equation above. Finally, the variables naturalFrequency and dampingRatio permit compliance to be introduced to a mimic joint in a manner that is mathematically analogous to a spring simulated with implicit first order integration. These two values default to value -1, which disables compliance. Mimic joint compliance is discussed in more detail in the accompanying document Mimic Joint Maths.
A mimic joint may be released using the function:
void PxArticulationMimicJoint::release();
It is important to note that mimic joints may only be created and released while the corresponding articulation instance is not part of a scene. In the absence of an explicit release() call, all mimic joints will be released when the corresponding articulation is itself released.
The gear ratio, offset, natural frequency and damping ratio may be updated in-between simulation steps:
void PxArticulationMimicJoint::setGearRatio(PxReal gearRatio);
void PxArticulationMimicJoint::setOffset(PxReal offset);
void PxArticulationMimicJoint::setNaturalFrequency(PxReal naturalFrequency);
void PxArticulationMimicJoint::setDampingRatio(PxReal dampingRatio);
The dofs coupled by a mimic joint, on the other hand, may only be be modified by first releasing the mimic joint and then recreating it.
A key feature of PhysX mimic joints is that limits and contacts are processed after mimic joints. This means that limits and contact constraints are preserved at the expense of mimic joints.
As mentioned previously, mimic joints support compliance. A general rule is that increasing both naturalFrequency and dampingRatio will make the mimic joint progressively stiffer and increase its ability to generate the impulse required to immediately resolve the mimic joint constraint. A mimic joint that is barely compliant, however, may lead to the kinds of unwanted instabilities discussed in section Articulation Drive Stability. A rule of thumb would be to choose dampingRatio to be greater than 1 in order to create overdamped compliance. The choice of natural frequency is linked to the choice of simulation timestep. As discussed in the accompanying document Mimic Joint Maths, mimic joint compliance follows a first order implicit formulation. An explicit time-stepping scheme would require the product of natural frequency and timestep to be less than 1 to allow multiple samples per oscillation. This is not the case with a first order formulation, which supports much larger values of naturalFrequency relative to the timestep.
As a final remark on mimic joints, it is worth noting that an articulation with a mimic joint may require many solver position iterations ( PxArticulationReducedCoordinate::setSolverIterationCounts()) to achieve good convergence, particularly if one of the joints of the mimic joint is driven by a stiff drive and the mimic joint either has stiff compliance or is configured as a hard constraint using the default values for dampingRatio and naturalFrequency. This is true for PxSolverType::eTGS and for PxSolverType::ePGS.
Link Incoming Joint Force
The SDK computes the spatial force transmitted by an articulation joint from parent to child link. Two example applications are:
Implementing a load-cell: A six-dof load cell can be placed between a robot arm and its end-effector to measure forces and torques applied by contacts to the end-effector. The load cell is straightforward to model as a fixed joint between robot arm and end-effector, and then querying the transmitted joint force.
Reinforcement-learning (RL) critic: An RL policy could evaluate forces transmitted through the joints of a walking robot in order to penalize policies that result in hardware-damaging impact forces.
Querying the Force
The transmitted force can be queried with the articulation cache flag PxArticulationCacheFlag::eLINK_INCOMING_JOINT_FORCE.
Note
The forces are reported in the joint frame of the link’s incoming joint. A benefit of this is that extracting, for example, the joint drive force/torque is a straightforward projection.
Forces Acting on an Articulation Link
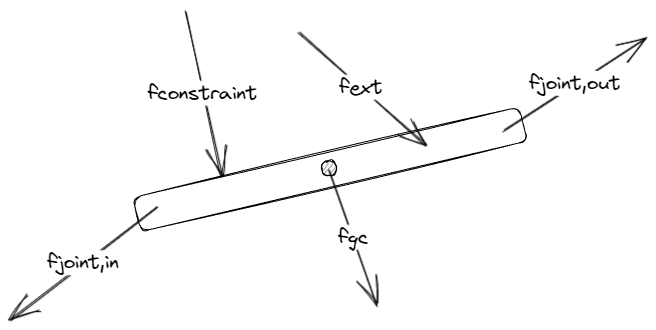
The spatial forces acting on an articulation link include:
\(f_{joint,in}\): The single incoming spatial joint force from the parent of the link.
\(f_{joint,out}\): The sum of the outgoing joint forces to child links (a link may have multiple children, but only one parent).
\(f_{gc}\): Gravitational and Coriolis force.
\(f_{ext}\): External forces including user-applied forces and torques, and link rigid-body velocity damping and clamping.
\(f_{constraint}\): External constraint forces such as contacts, or maximal-coordinate joint forces (e.g. D6 joint).
The reported force is equal to \(f_{joint,in}\). Note that the force is the average applied during the simulation step; therefore, the user has to be careful about inferring peak contact forces transmitted via joints since the reported force will be time-step-size dependent.
Detail on Included Forces
We include the following joint-internal force mechanisms in the reported force:
Joint Friction proportional to an approximation of the joint transmitted force applies a joint force/torque counteracting joint velocity, see
PxArticulationJointReducedCoordinate::setFrictionCoefficient().Joint Velocity Clamping applies a joint force/torque to clamp joint velocity, see
PxArticulationJointReducedCoordinate::setMaxJointVelocity().Joint Force/Torque can be applied directly by the user via the articulation cache
PxArticulationCacheFlag::eFORCE.Joint Drives apply joint forces/torques to drive the joint to a set position and velocity, see
PxArticulationJointReducedCoordinate::setDriveParams().Joint Limits apply joint forces/torques to keep the joint position within set limits, see
PxArticulationJointReducedCoordinate::setLimitParams().
We exclude the effects of
Fixed Tendons that apply joint forces/torques to drive a linear combination of joint dof positions to a desired target, see
PxArticulationFixedTendon. We may include the fixed tendon constraint forces in the joint force in a future version as they act on the joint dofs directly.Spatial Tendons that apply forces to articulation links at their root and leaf attachment in order to drive a linear combination of distances between tendon attachment points to a desired target, see
PxArticulationSpatialTendon.Armature that is additional inertia added to the link, and, depending on modeling, can show up as an apparent acceleration-resisting force/torque on the link, see the joint API
PxArticulationJointReducedCoordinate::setArmature().
Exclusion here means that we treat the effects analogous to external (constraint) forces or gravity, see sketch above, and not that the excluded forces are not considered in the computation of the transmitted joint force. See also example below of how a joint drive force appears in the reported incoming joint force.
Example
Consider a fixed-base articulation with a single revolute joint connecting a link to the base. The link rests on a static collider and a joint drive applies a torque. For simplicity, we assume that the joint frame aligns with the world frame.
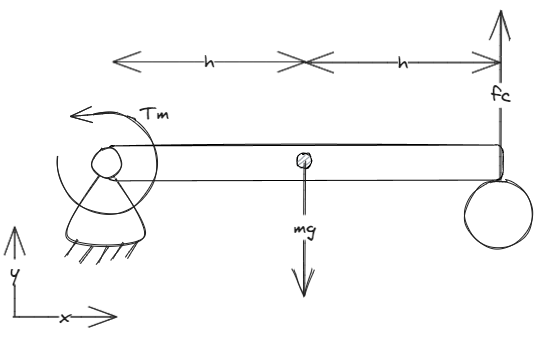
The torque transmitted by the joint is equal to the drive torque (in \(z\), all other elements are zero). We define the drive torque to be counteracting half of the gravitational torque at the pivot:
From a torque equilibrium in \(z\) at the pivot (for which we don’t need to know the joint force yet), we can determine the contact force \(f_c\):
The force transmitted by the joint has the single nonzero element \(f_y\) in \(y\). We can compute it with a force equilibrium:
Best Practices and Simulation Detail
Stability
The reduced coordinate articulations are suitable for use in games to simulate humanoids, i.e. ragdolls. However, introducing velocity clamps or damping may be required to ensure stability of the simulation at large angular velocities. The reason for this is the explicit integration of Coriolis and centrifugal forces. There are several options available to introduce damping and clamping by setting
rigid body velocity limits and damping; or
nonzero joint friction; or
adding a joint drive with nonzero damping
adding center-of-mass (COM) limits to the articulation
Inverse Dynamics, Jacobian and other Utility Computations
The reduced coordinate articulations offer inverse dynamics functionality in addition to forward dynamics used in simulation. This is a suite of utility functions to compute the joint forces required to counteract gravity, Coriolis/centrifugal force, external forces, and contacts/constraints. Furthermore, there are utility functions to compute kinematic Jacobians, the mass matrix, and the coefficient matrix and lambda values.
The following descriptions assume knowledge of inverse dynamics concepts.
Preparing the Articulation for Inverse Dynamics Computations
Prior to performing any inverse dynamics calculations, it is necessary to ensure that constant joint data has been computed. In order to do this, follow the steps
Set articulation pose (joint positions and base transform) via articulation cache and applyCache.
Depending on method: Setup base link velocity, and computation input values in cache.
Call inverse dynamics computation method, e.g.
PxArticulationReducedCoordinate::computeJointForce().
Converting From and To Reduced Coordinate Joint DOF Coordinates
The inverse dynamics functions operate on an articulation and a PxArticulationCache. The majority of properties in PxArticulationCache are stored in a reduced/generalized coordinate space, where one entry corresponds to a degree of freedom. To simplify working in this space, PhysX provides the following methods to pack and unpack data to convert between reduced/generalized and maximal coordinates.
Indexing: Indexing into the link maximum joint DOF data is via the link’s low-level index minus 1 (the root link is not included), and the reduced-coordinate DOF data follows the cache indexing convention, see Cache Indexing.
Example: Unpack a reduced-coordinate joint position of a fixed-base 1-DOF pendulum with a revolute joint with a free eSWING2 (z) motion:
PxReal maximalJointPositions[6] = { 0.0f };
PxReal reducedJointPosition = 0.5f;
articulation->unpackJointData(&reducedJointPosition, maximalJointPositions);
// Result: maximalJointPositions[PxArticulationAxis::eSWING2] is equal to 0.5f, and all other elements are 0.0f
Example: Pack maximal joint positions of a fixed-base 1-DOF pendulum with a revolute joint with a free eSWING2 (z) motion:
PxReal maximalJointPositions[6] = { 0.0f };
maximalJointPositions[PxArticulationAxis::eSWING2] = 0.5f;
PxReal reducedJointPosition = 0.0f;
articulation->packJointData(maximalJointPositions, &reducedJointPosition);
// Result: reducedJointPosition is equal to 0.5f
Gravity Compensation Force
Note
The PxArticulationReducedCoordinate::computeGeneralizedGravityForce has been deprecated and replaced with PxArticulationReducedCoordinate::computeGravityCompensation. With the deprecated method, it was not possible to obtain the gravity compensation forces of the root for floating-base articulations.
With:
articulation->computeGravityCompensation(*cache);
the forces required to counteract gravitational forces for the given articulation pose may be computed. The forces returned are determined purely by gravity for the articulation in the current joint and base pose, i.e. external forces, joint velocities, and joint accelerations are set to zero. In addition, any joint drives are not considered in the computation. The computed forces correspond to the (joint-space) “G(q)” term in the robotics manipulator equation.
For fixed-base articulations, the function returns the joint forces required to counteract gravitational forces, following the low-level joint DOF indexing, see Cache Indexing.
For floating-base articulations, the function returns the articulation root force and torque followed by the joint forces/torques (low-level joint DOF indexing).
This method, together with PxArticulationJointReducedCoordinate::computeMassMatrix() and PxArticulationJointReducedCoordinate::computeCoriolisCompensation(), can be used to calculate joint forces (and optionally root forces/torques) to achieve a given joint accelerations (and optionally root accelerations).
Inputs: Articulation pose (joint positions and base transform).
Outputs: Joint forces (and root force) to counteract gravity (in cache).
Example: Calculate holding torque to apply at a pendulum’s pivot when it is perpendicular to the gravity vector:
// set articulation pose to evaluate gravity forces at
cache->jointPosition[0] = PxPiDivTwo; // Set pendulum to be perpendicular to gravity
pendulumArticulation->applyCache(*cache, PxArticulationCacheFlag::ePOSITION);
// prepare common articulation data in newly set pose for inverse dynamics calculation
pendulumArticulation->commonInit();
pendulumArticulation->computeGravityCompensation(*cache);
PxReal massPendulum = 1.0f; // [kg]
PxReal distancePivotToCOM = 1.0f; // [m]
PxReal gravityMagnitude = 10.0f; // [m / s^2]
PxReal analyticHoldingTorque = massPendulum * distancePivotToCOM * gravityMagnitude; // [N * m]
PxReal computedHoldingTorque = cache->gravityCompensationForce[0]; // will be equal to analyticHoldingTorque = 10.0f
// we can now directly apply the computed torque; for example to gravity-compensate a simulated robot arm.
// make sure pendulum is at rest before simulation. Gravity compensation force should be copied to joint force.
cache->jointVelocity[0] = 0.0f;
const PxU32 dofCount = pendulumArticulation->getDofs();
PxMemCopy(cache->jointForce, cache->gravityCompensationForce, sizeof(PxReal) * dofCount);
pendulumArticulation->applyCache(*cache, PxArticulationCacheFlag::eVELOCITY | PxArticulationCacheFlag::eFORCE);
// simulate a single step
runSim(1);
// read out post-simulation joint velocity
art->copyInternalStateToCache(*cache, PxArticulationCacheFlag::eVELOCITY);
PxReal postSimVel = cache->jointVelocity[0]; // will be zero
Coriolis and Centrifugal Compensation Force
Note
The PxArticulationReducedCoordinate::computeCoriolisAndCentrifugalForce has been deprecated and replaced with PxArticulationReducedCoordinate::computeCoriolisCompensation. With the deprecated method, it was not possible to obtain the Coriolis and centrifugal compensation forces of the root for floating-base articulations.
With:
articulation->computeCoriolisCompensation(*cache);
the forces required to counteract Coriolis and centrifugal forces for the given articulation state may be computed. The forces returned are determined purely by the articulation’s state; i.e. external forces, gravity, joint accelerations and link accelerations are set to zero. Joint drives and potential damping terms, such as link angular or linear damping, or joint friction, are also not considered in the computation. The computed forces correspond to the (joint-space) “C(q,qdot) * qdot” term in the robotics manipulator equation.
For fixed-base articulations, the function returns the joint forces required to counteract Coriolis and centrifugal force, following the low-level joint DOF indexing, see Cache Indexing.
For floating-base articulations, the function returns the articulation root force and torque followed by the joint forces/torques (low-level joint DOF indexing).
This method, together with PxArticulationJointReducedCoordinate::computeMassMatrix() and PxArticulationJointReducedCoordinate::computeGravityCompensation(), can be used to calculate joint forces (and optionally root forces/torques) to achieve a given joint accelerations (and optionally root accelerations).
Inputs: Articulation state (joint positions and velocities (in cache), and base transform and spatial velocity).
Outputs: Joint forces (and root force) to counteract Coriolis and centrifugal forces (in cache).
To compute the joint force required to counteract Coriolis and centrifugal force, the joint velocities of the articulation must be provided as the Coriolis/centrifugal forces are dependent on those values. In this example, the velocities are extracted from the articulation before computing the Coriolis/centrifugal force:
articulation->copyInternalStateToCache(*cache, PxArticulationCache::eVELOCTY);
articulation->computeCoriolisCompensation(*cache);
Example: Calculate joint torques to keep a fixed-base double pendulum’s joint accelerations zero when the first link is rotating with 1 rad/s around the fixed pivot and with the second link perpendicular to the first (so that a centrifugal force has to be countered):
// initial joint states:
cache->jointPosition[0] = 0.0f; // does not matter
cache->jointPosition[1] = PxPiDivTwo; // perpendicular to first link
cache->jointVelocity[0] = 1.0f; // rotate at 1 rad/s
cache->jointVelocity[1] = 0.0f; // at rest relative to first link
// set articulation state (velocity not required for computation, but for later simulation from given state):
doublePendulum->applyCache(*cache, PxArticulationCacheFlag::ePOSITION | PxArticulationCacheFlag::eVELOCITY);
// prepare common articulation data for inverse dynamics calculation:
doublePendulum->commonInit();
// compute centrifugal torque (the joint velocities in the cache are used for the computation here)
doublePendulum->computeCoriolisCompensation(*cache);
// compute gravity compensation as well to keep acceleration zero:
doublePendulum->computeGravityCompensation(*cache);
// add centrifugal torque and gravity compensation
cache->jointForce[1] = cache->coriolisForce[1] + cache->gravityCompensationForce[1];
// apply torques at joints
doublePendulum->applyCache(*cache, PxArticulationCacheFlag::eFORCE);
// run one sim step and get post-sim joint velocities:
runSim(1);
doublePendulum->copyInternalStateToCache(*cache, PxArticulationCacheFlag::eVELOCITY);
PxReal postSimVelOne = cache->jointVelocity[0]; // will be 1 rad/s
PxReal postSimVelTwo = cache->jointVelocity[1]; // will be 0 rad/s
Generalized External Force
With:
articulation->computeGeneralizedExternalForce(*cache);
we can compute the joint DOF forces required to counteract external spatial forces applied to articulation links. Only the external forces and the current articulation pose are considered in the calculation.
The external spatial forces are with respect to the links’ centers of mass, and not the actor’s origin.
Inputs: External forces on links (in cache), articulation pose (joint positions + base transform).
Outputs: Joint forces to counteract the external forces (in cache).
Example: Compute joint torque at pendulum articulation pivot when spatial force is applied to the pendulum center of mass:
// set pendulum pose
// the angle is in +Z relative to upright where the pendulum coincides with +Y, and the pivot is at the origin.
PxReal pendulumAngle = PxPiDivFour;
cache->jointPosition[0] = pendulumAngle;
pendulum->applyCache(*cache, PxArticulationCacheFlag::ePOSITION);
// prep common articulation data for given pose for inverse dynamics computation
pendulum->commonInit();
// Define the spatial force to apply to the pendulum
// Note that this spatial force is defined with respect to the center of mass of the link
// which may or may not coincide with the actor frame origin (\see PxRigidBody::getCMassLocalPose)
PxSpatialForce force = PxSpatialForce();
force.force = PxVec3(1.0f, 0.0f, 0.0f); // acts on center of mass!
force.torque = PxVec3(0.0f, 0.0f, 1.0f);
PxArticulationLink* pendulumLink = nullptr;
// getLinks is indexed in order that the links were added to the articulation
PxU32 linkIndex = 1u;
PxU32 bufferSize = 1u;
pendulum->getLinks(&pendulumLink, bufferSize, linkIndex);
// external forces are indexed by low-level link index
// (for this simple articulation the low-level and getLinks indices will be equal)
cache->externalForces[pendulumLink->getLinkIndex()] = force;
pendulum->computeGeneralizedExternalForce(*cache);
// force in +X results in + counter torque and spatial torque in - counter torque
PxReal analyticCounterTorque = PxCos(pendulumAngle) * distancePivotToCOM * force.force.x - force.torque.z;
PxReal computedCounterTorque = cache->jointForce[0];
// analytic and computed are equal
Joint Accelerations from Joint Forces and Gravity
With:
articulation->computeJointAcceleration(*cache);
we can compute the joint accelerations for the given articulation state and joint forces, taking into account gravity. Joint drives and potential damping terms are not considered in the computation (for example, linear link damping or joint friction).
Inputs: Joint forces (in cache) and articulation state (joint positions and velocities (in cache), and base transform and spatial velocity).
Outputs: Joint accelerations (in cache).
Example: Compute joint accelerations at pendulum articulation pivot with and without applying a joint force:
// calculate pendulum inertia for computations below:
PxReal inertiaAtCOM = distancePivotToCOM * distancePivotToCOM * mass / 3.0f;
PxReal inertiaAtPivot = inertiaAtCOM + distancePivotToCOM * distancePivotToCOM * mass;
// Case 1: Pendulum perpendicular to gravity and zero input torque: Pivot acceleration will be due to gravity.
cache->jointPosition[0] = PxPiDivTwo; // gravity will result in a positive angular acceleration
pendulum->applyCache(*cache, PxArticulationCacheFlag::ePOSITION);
// prepare articulation data for the computation
pendulum->commonInit();
cache->jointForce[0] = 0.0f; // only consider acceleration due to gravity:
// For a more complex articulation than this simple example pendulum, the jointVelocity in the cache would have
// to be set for the computation of joint accelerations due to Coriolis terms.
pendulum->computeJointAcceleration(*cache);
PxReal torqueDueToGravityAtPivot = gravityMagnitude * mass * distancePivotToCOM;
PxReal analyticAcceleration = torqueDueToGravityAtPivot / inertiaAtPivot;
PxReal computedAcceleration = cache->jointAcceleration[0];
// analytic and computed are equal
// Case 2: Apply a torque to cancel the gravitational joint acceleration:
cache->jointForce[0] = -torqueDueToGravityAtPivot; // 1 Nm input
// running computation with same articulation pose as Case 1, so no need to call commonInit again.
pendulum->computeJointAcceleration(*cache);
analyticAcceleration = 0.0f;
computedAcceleration = cache->jointAcceleration[0];
// analytic and computed are equal
Joint Forces from Joint Accelerations without Gravity
With:
articulation->computeJointForce(*cache);
we can compute the joint forces required to achieve desired joint DOF accelerations for the given articulation state, not considering gravity. Joint drives and potential damping terms are not considered in the computation (for example, linear link damping or joint friction).
This method, together with PxArticulationJointReducedCoordinate::computeGravityCompensation(), can be used to calculate feed-forward joint forces to apply to follow a reference joint-space trajectory using feedback control.
Inputs: Joint accelerations (in cache) and articulation state (joint positions and velocities (in cache), and root transform and spatial velocity).
Outputs: Joint forces (in cache).
Example: Compute joint forces at pendulum articulation pivot in order to achieve a desired angular acceleration:
// calculate pendulum inertia for computations below:
PxReal inertiaAtCOM = distancePivotToCOM * distancePivotToCOM * mass / 3.0f;
PxReal inertiaAtPivot = inertiaAtCOM + distancePivotToCOM * distancePivotToCOM * mass;
// Pendulum angle will not matter because gravity is not considered in the computation
// so directly prepare articulation data for the computation
pendulum->commonInit();
PxReal targetAcceleration = 1.0f; // rad/s^2
cache->jointAcceleration[0] = targetAcceleration;
// For a more complex articulation than this simple example pendulum, the cache jointVelocity member would have
// to be set for the computation of joint accelerations due to Coriolis terms
pendulum->computeJointForce(*cache);
PxReal analyticTorque = targetAcceleration * inertiaAtPivot;
PxReal computedTorque = cache->jointForce[0];
// analytic and computed are equal
Articulation Center of Mass
With:
PxVec3 articulationCOM = articulation->computeArticulationCOM(rootFrame);
the articulation’s center of mass may be computed in either the world frame (default) or root frame (if rootFrame = true).
The computation uses the current pose of the articulation, which can be changed using PxArticulationReducedCoordinate::applyCache().
Inputs: Articulation state (joint positions and root transform).
Outputs: Articulation’s center of mass in either the world frame (default) or root frame.
Example: Compute a pendulum’s center of mass using a new joint pose:
// Set a new pose for the pendulum (optional)
PxReal pendulumAngle = PxPiDivFour;
cache->jointPosition[0] = pendulumAngle;
pendulum->applyCache(*cache, PxArticulationCacheFlag::ePOSITION);
// Compute the pendulum center's of mass in the world frame
PxVec3 pendulumCOM = pendulum->computeArticulationCOM();
Generalized Mass Matrix
Note
The PxArticulationReducedCoordinate::computeGeneralizedMassMatrix has been deprecated and replaced with PxArticulationReducedCoordinate::computeMassMatrix. With the deprecated method, it was not possible to achieve a desired root acceleration for floating-base articulations.
With:
articulation->computeMassMatrix(*cache);
the generalized mass matrix may be computed. In the absence of gravity and Coriolis effects, the mass matrix can be used to convert accelerations into forces/torques, i.e. forces = massMatrix * accelerations. The mass matrix corresponds to the \(M(q)\) term in the robotics manipulator equation.
For fixed-base articulations, the accelerations vector and forces vector are composed of the joint accelerations and joint forces/torques, respectively, following the low-level joint DOF indexing, see Cache Indexing.
In this case, the mass matrix has a size of (nbDofs * nbDofs) where nbDofs is the number of degrees of freedom of the articulation.
For floating-base articulations, the accelerations vector is composed of the articulation root acceleration (linear, then angular components) followed by the joint accelerations (low-level joint DOF indexing).
The forces vector is composed of the articulation root force then torque followed by the joint forces/torques (low-level joint DOF indexing). Therefore, the forces and acceleration vectors are of size nbDofs + 6 and the mass matrix is of size ((nbDofs + 6) * (nbDofs + 6)) where nbDofs is the number of degrees of freedom of the articulation.
This method, together with PxArticulationJointReducedCoordinate::computeGravityCompensation() and PxArticulationJointReducedCoordinate::computeCoriolisCompensation(), can be used to calculate the joint and root forces/torques required to achieve desired joint and root accelerations.
Inputs: Articulation pose (joint positions and base transform).
Outputs: The generalized mass matrix (in cache).
Note that the mass matrix is indexed row-major as [nCols * row + column] where nCols is equal to nbDofs or nbDofs + 6 for fixed-base and floating-base articulations, respectively.
Centroidal Momentum Matrix and Bias Force
With:
articulation->computeCentroidalMomentumMatrix(*cache);
the centroidal momentum matrix \(A_G\) and the corresponding bias force \(\dot{A}_G \dot{q}\) are computed. The centroidal momentum and bias can be applied to humanoid robot whole-body control, see the references in the notes below.
These computed matrix and bias can be used to predict the evolution of the centroidal momentum \(h_G\) using the velocity \(\dot{q}\) and acceleration \(\ddot{q}\) of the combined root-link and joint degrees-of-freedom of a floating-base articulation:
and
The centroidal momentum matrix has a size of (6 * (nbDofs + 6)), and the bias force has size 6.
Inputs: Articulation state (joint positions and velocities and base transform and spatial velocity); Generalized Mass Matrix; and Coriolis and Centrifugal Compensation Force.
Outputs: The centroidal momentum matrix and bias force (in cache).
Note
The centroidal momentum matrix is indexed row-major as
[nCols * row + column], wherenColsis equal tonbDofs + 6and eachrowcorresponds to an element of the .This function assumes that up-to-date values for the Generalized Mass Matrix and the Coriolis and Centrifugal Compensation Force are present in the cache. They can be computed with
PxArticulationReducedCoordinate::computeMassMatrix()andPxArticulationReducedCoordinate::computeCoriolisCompensation()respectively.For reference, see Wensing et al. and Orin et al..
This method is only applicable to floating-base articulations.
Loop Joints, Coefficient Matrix, and Lambda Constraint Impulses
Note
The loop-joint and related coefficient and lambda impulse API is deprecated and will be removed in a future version once a substitute feature is in place. Please refer to the previous version’s documentation for more information on the deprecated features.
Jacobian
The Jacobian matrix is an important concept for robotics and used, for example, in inverse kinematics computation. Multiplication with the Jacobian matrix maps the joint space velocities of the robot to world-space link velocities. The Jacobian matrix of an articulation can be computed using:
PxU32 nRows;
PxU32 nCols;
articulation->computeDenseJacobian(*cache, nRows, nCols);
This will write the Jacobian matrix to cache.denseJacobian; and the dimensions of the matrix are written to the two unsigned integers. Note that the Jacobian matrix is a sparse triangular matrix, so such an explicit dense representation is in general not an optimal use of memory. PhysX does not use this representation internally.
The spatial link velocities that the matrix maps to are with respect to the center of mass (COM) of the links, and are stacked [vx; vy; vz; wx; wy; wz], where vx and wx refer to the linear and rotational velocity in world X, respectively.
- Indexing:
Links, i.e. rows are in order of the low-level link indices (minus one if PxArticulationFlag::eFIX_BASE is true), see PxArticulationLink::getLinkIndex().
DOFs, i.e. column indices correspond to the low-level DOF indices, see Cache Indexing.
Example: Jacobian of a 1-DOF, single-link pendulum:
// setup perpendicular to gravity (-g * eY), and pointing in -eX direction away from pivot
cache->jointPosition[0] = PxPiDivTwo;
pendulum->applyCache(*cache, PxArticulationCacheFlag::ePOSITION);
PxU32 nRows = 0u;
PxU32 nCols = 0u;
pendulum->computeDenseJacobian(*cache, nRows, nCols);
// nRows will be equal to 6, as the fixed-base articulation has a single free link
// nCols will be equal to 1, as the pendulum has a single degree of freedom
// for a given joint velocity w in eZ and the given pendulum angle of 90deg,
// the spatial velocity of the pendulum only has two nonzero elements:
// vy = -w * distancePivotToCOM <- because the spatial velocity is with respect to the COM of the pendulum
// wz = w <- trivially the rotational velocity of the pivot joint
// The Jacobian is the partial derivative of the spatial velocity with respect to w, so the matrix will be:
// Jac[0, 0] = dvx / dw = 0
// Jac[1, 0] = dvy / dw = -distancePivotToCOM
// Jac[2, 0] = dvz / dw = 0
// Jac[3, 0] = dwx / dw = 0
// Jac[4, 0] = dwy / dw = 0
// Jac[5, 0] = dwz / dw = 1
// this is overkill for this simple articulation but shows how to calculate the row index for a more
// complex fixed-base articulation. Not done here, but the user in general has to follow the snippet in the
// Cache Indexing section above in order to find the low-level DOF index.
PxArticulationLink* pendulumLink = nullptr;
PxU32 linkIndex = 1u; // getLinks is indexed in order that the links were added to the articulation
PxU32 bufferSize = 1u;
pendulum->getLinks(&pendulumLink, bufferSize, linkIndex);
PxU32 dofColumn = 0; // relevant column is the 0-th one that corresponds to the single DOF of the pendulum
// -1 on the low-level link index as the fixed base link is not included
PxU32 vyRow = ((pendulumLink->getLinkIndex() - 1) * 6) + 1;
PxU32 wzRow = ((pendulumLink->getLinkIndex() - 1) * 6) + 5;
PxReal jac10 = cache->denseJacobian[nCols * vyRow + dofColumn]; // equal to -distancePivotToCOM
PxReal jac50 = cache->denseJacobian[nCols * wzRow + dofColumn]; // equal to 1