Soft Bodies

Introduction

As opposed to rigid bodies, which preserve the relative poses of their vertex representation, soft bodies support relative motion of the nodes governing their form. A consequence of this complexity is that soft bodies deform under applied force, while rigid bodies do not. PhysX soft body simulation employs a combination of FEM (Finite Element Method) and two tetrahedral meshes. The first tetrahedral mesh is a simulation mesh, which only needs to approximately match the body’s shape. This freedom allows the use of meshes with more regular and equal-sized tetrahedra. The second tetrahedral mesh is the collision mesh. The collision mesh needs to match the surface of the simulated body accurately, otherwise the collision response will not be accurate. In addition to the simulation and collision meshes, there is also an associated triangle mesh that is used for rendering. The render mesh is typically used to generate the collision mesh. To achieve a smooth deformation the render mesh should have uniformly distributed vertices.

Given that TGS offers better convergence with a computational cost comparable to PGS, TGS is recommended for soft body simulation (Macklin et al., 2019).

Tet Maker

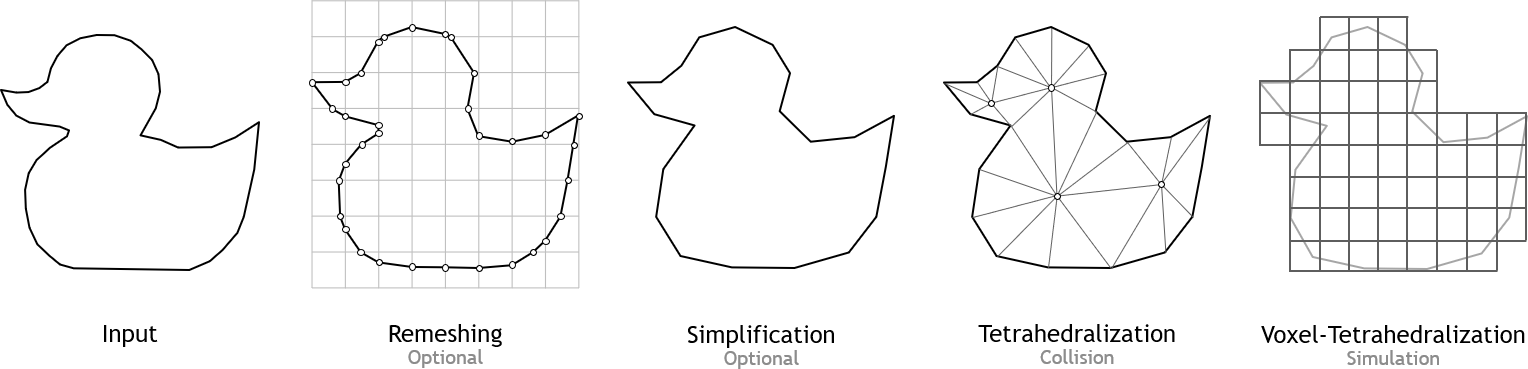
The tetrahedral meshes required to create a soft body can be provided either from an external source or they can be created directly in PhysX by a component called Tet Maker. This process can be time consuming, therefore it is recommended to do it as a preprocessing step and save the cooked meshes to a file. The collision mesh is typically created from the render mesh by calling createConformingTetrahedronMesh(…). The surface of the resulting tetrahedral mesh will exactly match the surface of the input triangle mesh. The vertex list of the collision mesh replicates all vertices from the render mesh. The mesher can append additional vertices in case this is required to generate a valid tetrahedral mesh. The simulation mesh can be created by calling createVoxelTetrahedronMesh(…) which takes the previously generated collision mesh as input as well as parameters to define the resolution of the output mesh. It will create voxels completely enclosing the collision mesh. The following image shows the render mesh, the collision tetmesh and the simulation tetmesh from left to right.

There are a few variables for users to control the resolution of the mesh and to get optional embedding information:

numVoxelsAlongLongestBoundingBoxAxis: Allows control over the resolution of the resulting mesh. The parameter specifies the number of voxels to generate along the longest axis of the input mesh’s bounding box. The number of cells along the smaller dimensions will be computed such that voxels get similar edge lengths in all directions.
numTetsPerVoxel: Every voxel will be split into 5 or 6 tetrahedra to produce a mesh with elements of similar size and shape.
inputPointToOutputTetIndex: This is an optional parameter that allows a mapping between input point and the tetrahedron containing the point. If NULL is passed in, that information is not generated, otherwise pointer to a list with size matching the number of input vertices can be provided.

The example in the section Using GPU Soft Bodies shows how to generate both meshes.

Mesh Cleaning

Some triangle meshes contain holes, self intersections, sliver triangles (triangles where at least one angle is much bigger or much smaller than the other angles) or other defects. Generating a tetmesh out of a triangle mesh that has defects might not be possible or lead to a bad tetmesh. In that case a remeshing operation can help to fix the mesh defects. Other triangle meshes might simply have an excessive amount of triangles such that it makes sense to reduce the mesh’s resolution before generating a collision and a simulation tetmesh. The high resolution triangle mesh can still be used for rendering.

The following piece of code shows how to create a new set of vertices and triangles using a remeshing operation to fix mesh defects:

PxArray<PxVec3> inputVertices;
PxArray<PxU32> inputIndices;
PxArray<PxVec3> outputVertices;
PxArray<PxU32> outputIndices;
PxI32 remesherGridResolution = 100;
PxTetMaker::remeshTriangleMesh(inputVertices, inputIndices, remesherGridResolution, outputVertices, outputIndices);

A remeshing operation might increase the number of triangles. This depends on the resolution of the internal grid that the remesher uses. In many cases it makes sense to reduce the number of triangles to a number that still captures the mesh’s surface well while being as low as possible because the less triangles, the less tetrahedra the collision tetmesh will have and the faster the simulation will run. The following code shows how to reduce the number of triangles in a mesh to a given target. It does not make use of the maximal edge length feature that allows to avoid too long triangle edges because big triangles don’t approximate the body’s shape well when it starts deforming:

PxArray<PxVec3> inputVertices;
PxArray<PxU32> inputIndices;
PxArray<PxVec3> outputVertices;
PxArray<PxU32> outputIndices;
PxI32 targetTriangleCount = 500;
PxReal maximalTriangleEdgeLength = 0.0f;
PxTetMaker::simplifyTriangleMesh(inputVertices, inputIndices, targetTriangleCount, maximalTriangleEdgeLength, outputVertices, outputIndices);

All mesh processing steps are usually performed in the following order

Remeshing (optional)

Mesh Simplification (optional)

Creation of collision tetmesh

Creation of simulation tetmesh using the voxel tetmesher

Cooking

During the cooking process, all internal structures required by the simulation are configured. This includes acceleration structures for collision detection; ordering and partitioning for the tetrahedra mesh; mass/volume properties for every vertex/tetrahedra of the simulation mesh; and remap tables to update the collision mesh’s vertices according to the simulation mesh’s deformation. This precomputed data must be updated if the topology of the soft body is changed by the application at runtime e.g. due to tearing/cutting. Density, uniform scaling and translation are defined when the softbody is constructed.

Depending on the mesh’s resolution, cooking might take some time. To avoid calculating this data every time a simulation starts, the cooked data can be saved to a file by calling cookSoftbodyMesh. To load the cooked file, the PxPhysics instance provides a createSoftbodyMesh method that takes a file stream as source:

//Cook and save the mesh
PxDefaultFileOutputStream writeBuffer(cacheFilename);
bool status = PxCookSoftBodyMesh(cookingParams, simMeshDesc, meshDesc, simDesc, writeBuffer);

//Load the cooked mesh
PxDefaultFileInputData readBuffer(cacheFilename);
tetMesh = getPhysics().createSoftbodyMesh(readBuffer);

Using GPU Soft Bodies

PhysX soft bodies are currently only supported on GPU. This feature is implemented in CUDA and requires a compatible GPU. If no compatible device is found, an error message will be displayed. The following snippet shows how to create a softbody from scratch given only triangle mesh vertices and indices. Separate collision and simulation meshes are used in the snippet. It is also possible to use the same mesh as simulation and collision mesh:

//Compute collision mesh
physx::PxArray<physx::PxVec3> collisionMeshVertices, simulationMeshVertices;
physx::PxArray<physx::PxU32> collisionMeshIndices, simulationMeshIndices;
PxTetMaker::createConformingTetrahedronMesh(surfaceMesh, collisionMeshVertices, collisionMeshIndices);
PxTetrahedronMeshDesc meshDesc(collisionMeshVertices, collisionMeshIndices);

//Compute simulation mesh
PxU32 numVoxelsAlongLongestAABBAxis = 20;
physx::PxArray<physx::PxI32> vertexToTet;
vertexToTet.resize(meshDesc.points.count);
PxTetMaker::createVoxelTetrahedronMesh(meshDesc, numVoxelsAlongLongestAABBAxis, simulationMeshVertices, simulationMeshIndices, vertexToTet.begin());
PxTetrahedronMeshDesc simMeshDesc(simulationMeshVertices, simulationMeshIndices);
PxSoftbodySimulationDataDesc simDesc(vertexToTet);

PxSoftbodyMesh* mesh = PxCreateSoftBodyMesh(cookingParams, simMeshDesc, meshDesc, simDesc, getPhysics().getPhysicsInsertionCallback());

PxSoftBody* softBody = getPhysics().createSoftBody(*mCudaContextManager);
PxShapeFlags shapeFlags = PxShapeFlag::eVISUALIZATION | PxShapeFlag::eSIMULATION_SHAPE;
PxFEMSoftBodyMaterial* materialPtr = getPhysics().createFEMSoftBodyMaterial(1e+9f, 0.45f, 0.5f);
PxTetrahedronMeshGeometry geometry(mesh->getCollisionMesh());
PxShape* shape = getPhysics().createShape(geometry, &materialPtr, 1, true, shapeFlags);
softBody->attachShape(*shape);
softBody->attachSimulationMesh(*mesh->getSimulationMesh(), *mesh->getSoftBodyAuxData());
getActiveScene().addSoftBody(*softBody);

After the soft body has been added to the scene, the GPU data needs to be initialized and copied to the GPU. We provide a set of extension functions in PxSoftBodyExt that serve as a starting point. First, pinned host memory buffers to mirror the data have to be allocated and initialized:

PxVec4* simPositionInvMassPinned;
    PxVec4* simVelocityPinned;
    PxVec4* collPositionInvMassPinned;
    PxVec4* restPositionPinned;

PxSoftBodyExt::allocateAndInitializeHostMirror(*softBody, mCudaContextManager, simPositionInvMassPinned, simVelocityPinned, collPositionInvMassPinned, restPositionPinned);

Ownership of the pinned host buffers is transferred to the user, who is responsible for freeing these buffers during the shutdown procedure. To adjust location, orientation and scaling of a softbody after cooking, an optional call to transform will modify the internal softbody buffers accordingly:

PxSoftBodyExt::transform(*softBody, transform, scale, simPositionInvMassPinned, simVelocityPinned, collPositionInvMassPinned, restPositionPinned);

The maximal inverse mass ratio specifies how much the mass at connected vertices is allowed to vary. Big mass ratios in the mesh can be bad for the simulation stability and convergence. To ensure that the body has a properly defined mass, either total mass or mass density must be specified:

PxSoftBodyExt::updateMass(*softBody, density, maxInvMassRatio, simPositionInvMassPinned);

Finally, the softbody buffers need to be uploaded to the GPU. This can either be done by calling Cudamemcpy for every buffer to upload or more easily using the copyToDevice method from the softbody extensions:

PxSoftBodyExt::copyToDevice(*softBody, PxSoftBodyDataFlag::eALL, simPositionInvMassPinned, simVelocityPinned, collPositionInvMassPinned, restPositionPinned);

In addition to the softbody geometry, a few solver settings should be configured. The section about tuning provides more details:

softBody->setParameter(femParams);
softBody->setSolverIterationCounts(iterCount);

Kinematic Soft Bodies

Softbodies support user-driven movements similar to kinematic rigid bodies. In addition a softbody can be partially kinematic. A partially kinematic softbody has kinematic targets specified for some of its vertices while others can move freely (the solver will update their location to minimize the softbody’s internal stress). PhysX ensures that vertices that got moved kinematically get the correct velocity assigned which is important for good collision responses.

One of the main use cases for partially kinematic softbodies are animated characters where the movement of the skin (often the skin is a time-sampled triangle mesh) is pre-defined but the body should still interact with the world, e. g. a shirt over the skin should show correct physical behavior and move with the animated object through collisions. The main advantage of using a softbody for this interaction is that they are space filling which makes collision detection more robust.

The setup of a fully or partially kinematic softbody is similar to a normal soft body but requires a couple of additional steps.

A fully kinematic softbody expects a kinematic target to be set for every simulation vertex whereas a partially kinematic softbody only expects a valid kinematic target for simulation mesh vertices with an inverse mass of zero. An inverse mass of zero means the vertex cannot be moved by the solver. This is desired since constrained vertices that have a kinematic target should not move since it’s the users responsibility to place them. The number of elements in the kinematic target buffer is always equal to the number of vertices in the simulation tetmesh. The preparation of kinematic targets can be done as follows:

PxVec4* kinematicTargets = PX_EXT_PINNED_MEMORY_ALLOC(PxVec4, *cudaContextManager, vertexCount);
PxVec4* positionInvMass = sb->mPositionsInvMass;
for (PxU32 i = 0; i < vertexCount; ++i)
{
    PxVec4& p = positionInvMass[i];

    //Fix a couple of vertices
    if (p.y > 9.9f)
        p.w = 0.0f;
    if (p.y < 0.1f)
        p.w = 0.0f;

    kinematicTargets[i] = positionInvMass[i];
}

PxVec4* kinematicTargetsD = PX_EXT_DEVICE_MEMORY_ALLOC(PxVec4, *cudaContextManager, vertexCount);
cudaContextManager->getCudaContext()->memcpyHtoD(reinterpret_cast<CUdeviceptr>(softBody->getSimPositionInvMassBufferD()), positionInvMass, vertexCount * sizeof(PxVec4));
cudaContextManager->getCudaContext()->memcpyHtoD(reinterpret_cast<CUdeviceptr>(kinematicTargetsD), kinematicTargets, vertexCount * sizeof(PxVec4));

The user owns the kinematic target buffers and therefore is responsible to release their memory when they are not used anymore. To update the kinematic targets, one just executes the last line of the above snippets again to copy new kinematic targets to the gpu.

As last step of the setup process, the gpu buffer holding the kinematic targets must be registered:

softBody->setKinematicTargetBufferD(kinematicTargetsD, PxSoftBodyFlag::ePARTIALLY_KINEMATIC);

It usually makes sense to use the same simulation and collision tetmesh for a kinematic softbody (no voxel simulation mesh) because this setup simplifies the transfer of the animated motion to the softbody’s kinematic targets which is the users responsibility. To improve performance, it is possible to use the mesh simplifier to create a mapping that allows to drive a lower resolution softbody with a high resolution animated skin mesh.

Constitutive Model

To simulate soft body deformation, a version of corotated linear elasticity is used that inherits the simplicity of linear models while enforcing rotational invariance. A commonly used corotated model has the following form:

\[\Psi(\mathbf{F}) = \mu \| \mathbf{F} - \mathbf{R} \|_F^2 + \frac{\lambda}{2} \operatorname{tr}^2(\mathbf{R}^T\mathbf{F} - \mathbf{I})\]

\(\mathbf{F}\): The deformation gradient.

\(\Psi\): The energy density function of \(\mathbf{F}\).

\(\mathbf{R}\): The rotational component of \(\mathbf{F}\) (\(\mathbf{F}\) = \(\mathbf{R} \mathbf{S}\)).

\(\mathbf{I}\): The Identity matrix.

\(\lambda\), \(\mu\): The Lamé parameters.

\(\operatorname{tr(\cdot)}\): The trace of a matrix.

\(\operatorname{det(\cdot)}\): The determinant of a matrix.

\(\| \cdot \|_F^2\): The Frobenius norm of a matrix.

The first term resists stretching and compression and often referred as the As-Rigid-As-Possible (ARAP) energy, and the second term is to preserve the volume. PhysX uses a similar energy model to the corotated linear model, but incorporates a different volume coservation term as shown below:

\[\Psi(\mathbf{F}) = \mu \| \mathbf{F} - \mathbf{R} \|_F^2 + \frac{\lambda}{2} (\operatorname{det}(\mathbf{F}) - 1)^2.\]

This energy model is often referred to as the fixed corotated model.

Tuning

As illustrated in Constitutive Model, the material behaviors are controlled by the Lamé parameters in the energy density function: \(\mu\) for the first term (ARAP energy) and \(\lambda\) for the second term (volume-preserving energy). However, many physics simulators including PhysX use an equivalent set of parameters: Young’s modulus \(E\) and Poisson’s ratio \(\nu\), where

\[\begin{split}\mu &= \frac{E}{2(1 + \nu)} \\ \\ \lambda &= \frac{E \nu}{(1 + \nu)(1 - 2\nu)}.\end{split}\]

Practically speaking, increasing Young’s modulus \(E\) effectively makes the soft body stiffer, while a higher value of Poisson’s ratio \(\nu \in [0, 0.5]\) enforces better incompressibility. Using a value of 0.5 for the Poisson’s ratio means enforcing full incompressibility (i.e., applying infinite stiffness to the volume-preserving term). These material properties are controlled via PxFEMMaterial.

Additionally, the effect of damping can be added by setting a non-zero value for damping via PxFEMSoftBodyMaterial::setDamping().

Performance Considerations

To improve performance, it is advisable to choose tetrahedral meshes with the lowest resolution that delivers satisfactory results. At each simulation timestep, a stress measure is evaluated for each tetrahedron. The resolution of a mesh, therefore, has a direct impact on the computational effort required to update the deformation. Very stiff materials typically require more solver iterations to achieve convergence. Using a lower resolution simulation mesh often helps to simulate stiff objects, while keeping the required number of iterations low. To reduce the number of tetrahedra it is worth considering a collision mesh with very few interior nodes.

References

MACKLIN M., STOREY K., LU M., TERDIMAN P., CHENTANEZ N., JESCHKE S., MÜLLER M.: Small steps in physics simulation. In Proceedings of the 18th Annual ACM SIGGRAPH/Eurographics Symposium on Computer Animation (New York, NY, USA, 2019), SCA ’19, Association for Computing Machinery. URL: https://doi.org/10.1145/3309486.3340247, doi:10.1145/3309486. 3340247. 3, 4