What Is LIVERPS?#
A Note About LIVERPS vs LIVRPS
OpenUSD recently introduced a new composition arc called “relocates,” which is now included in the strength ordering acronym. What was previously known as LIVRPS is now LIVERPS, with the “E” representing rElocates. Learn OpenUSD will be updated soon to cover relocates, but for now, please note that you may see both LIVRPS and LIVERPS used interchangeably.
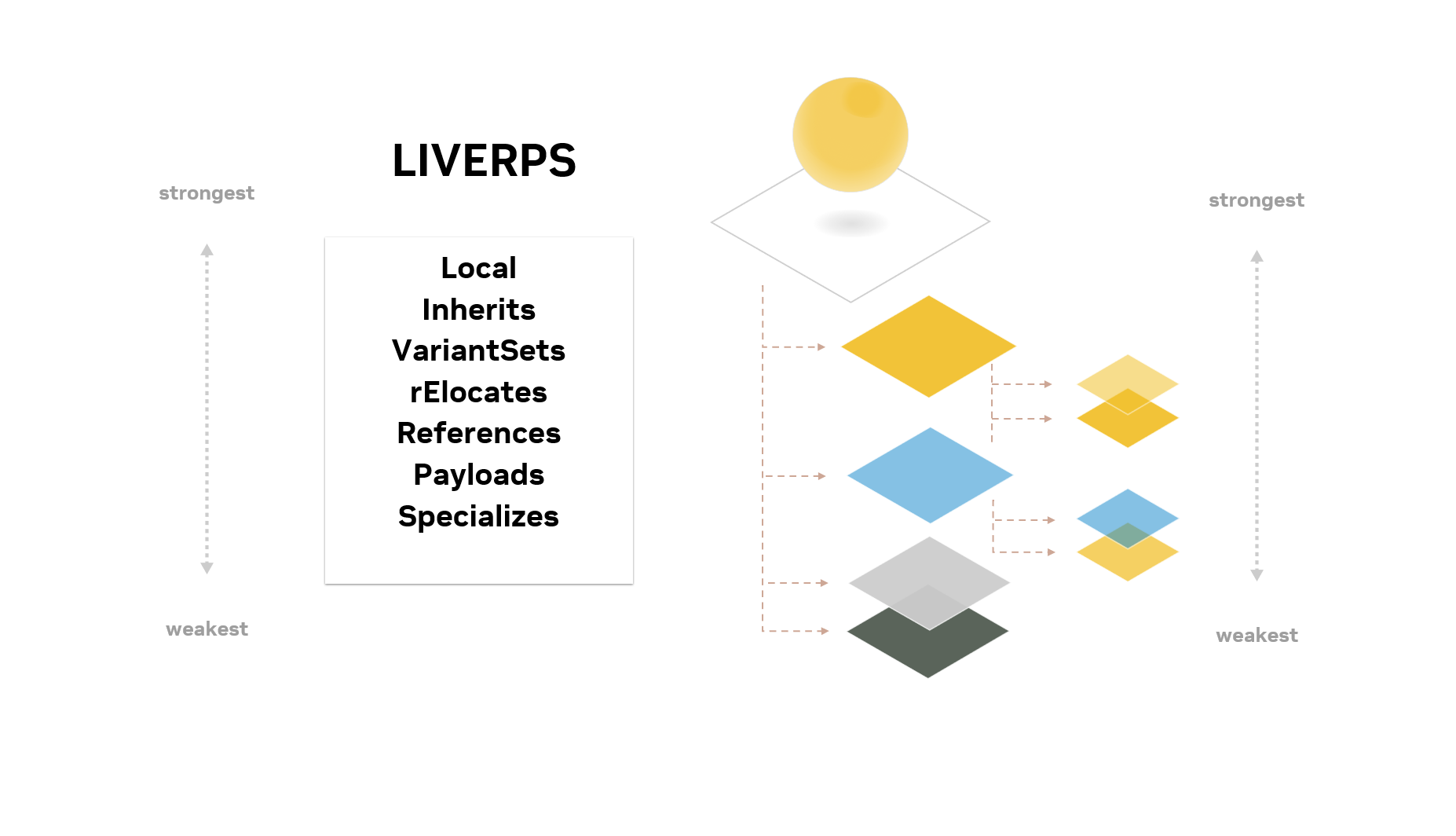
Throughout this course, we’ve been talking about individual composition arcs and talking about how some are stronger or weaker than others. These arcs adhere to a set of strength ordering rules that we affectionately refer to as LIVRPS (pronounced “liver peas”), an acronym that captures the individual arcs according to their strength, with local opinions being the strongest and specializes arcs being the weakest.
The LIVRPS acronym captures all of the operations to compose data from layers onto the stage, in the order in which each operation is applied.
Why do we need strength ordering rules? In OpenUSD, multiple layer stacks and their opinions are composed together to create the composed stage. We need strength ordering to determine which opinion gets composed in the final stage.
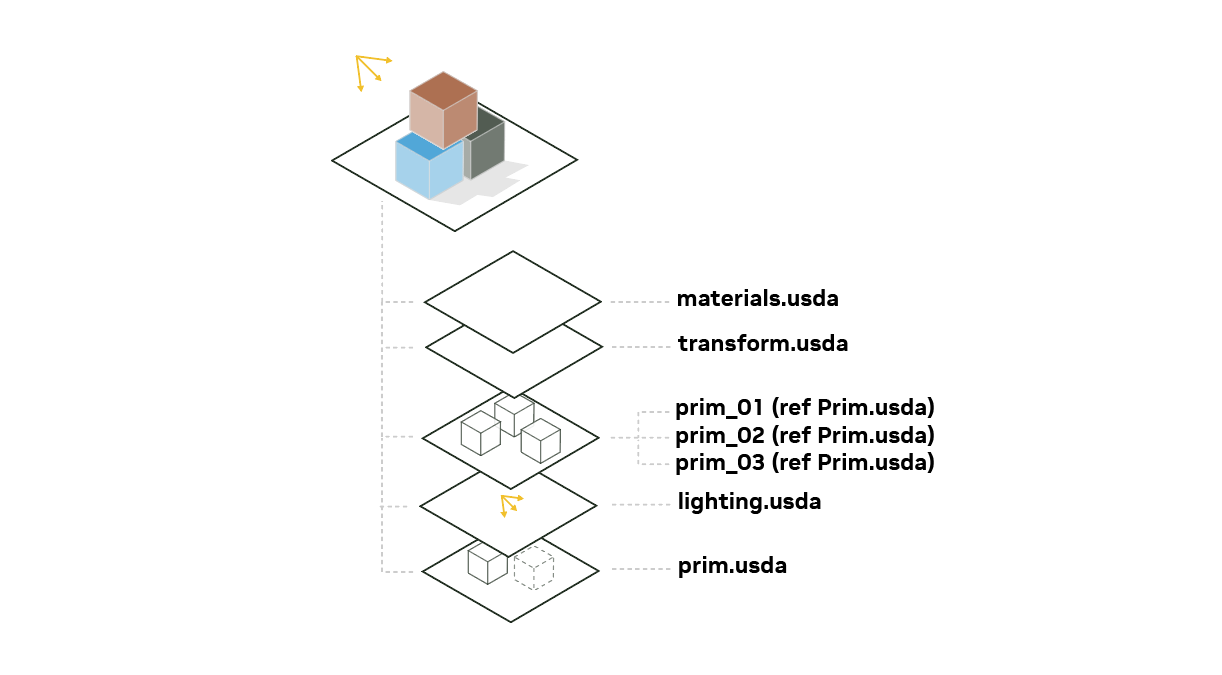
What is Layer Stack?
A layer stack is the ordered set of layers resulting from the recursive gathering of all sublayers of a layer, plus the layer itself as first and strongest. This also includes all local composition arcs like internal references, internal payloads, variant sets, inherits, and specializes. Multiple layer stacks are composed together using references and payloads.
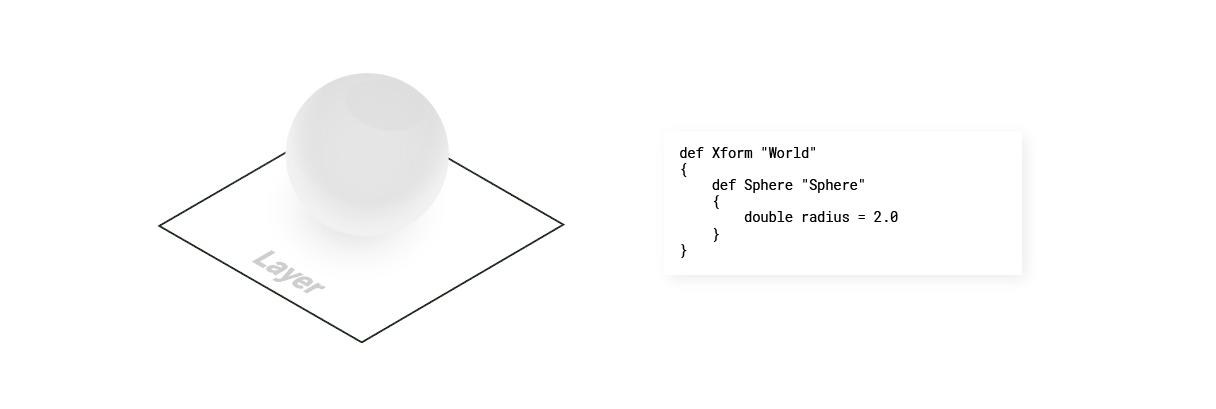
A local opinion is authored directly, without any other composition operations, in a layer or any of its recursive sublayers.
In the USDA file on the right, we have a local opinion which is our radius on our sphere.

In this stage with one layer, there is only one primSpec and propertySpec for the Sphere prim, so the composition is obvious. The composition is just the radius of the sphere, 2.0.

In the case where a layer has a sublayer, opinions authored directly in both layers are considered “local”.
Since we have an override on the sphere where the radius is 2.0, this is our local opinion on the root layer. This is stronger than the sublayer’s local opinion setting the radius to 1.0.
For any given layer stack, the opinion of the root layer is considered the strongest, followed by any opinions that appear in the ordered list of sublayers.

The local (L) component of LIVRPS also consists of all sublayers of sublayers as they all belong to the same layer stack. When opinion strength is evaluated, the strength-ordered list of sublayers is populated by recursively gathering sublayer opinions in a depth-first order.

In this case, sublayer1.usda is higher in the list than sublayer2.usda. Therefore, the opinions in sublayer1A.usda and sublayer1B.usda are stronger than opinions in sublayer2.usda, because they are sublayers of sublayer1.usda.
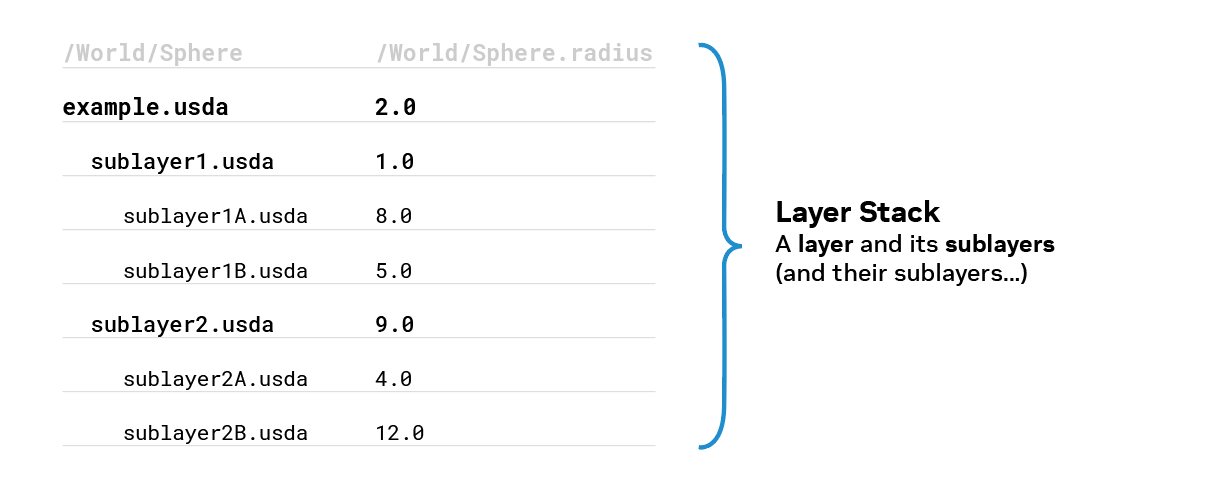
Now let’s think about this as a layer stack. A layer stack consists of a layer and all of its recursive sublayers. Any direct opinion authored in any layer in the stack is considered local to that layer stack.
It’s important to note that composition operations, such as references and payloads, are considered in the context of a layer stack, not an individual layer.

LIVRPS answers the questions–given a prim on a USD stage, how do I build the primSpec stack that represents it? How do you build propertySpec stacks for the properties on the prim?
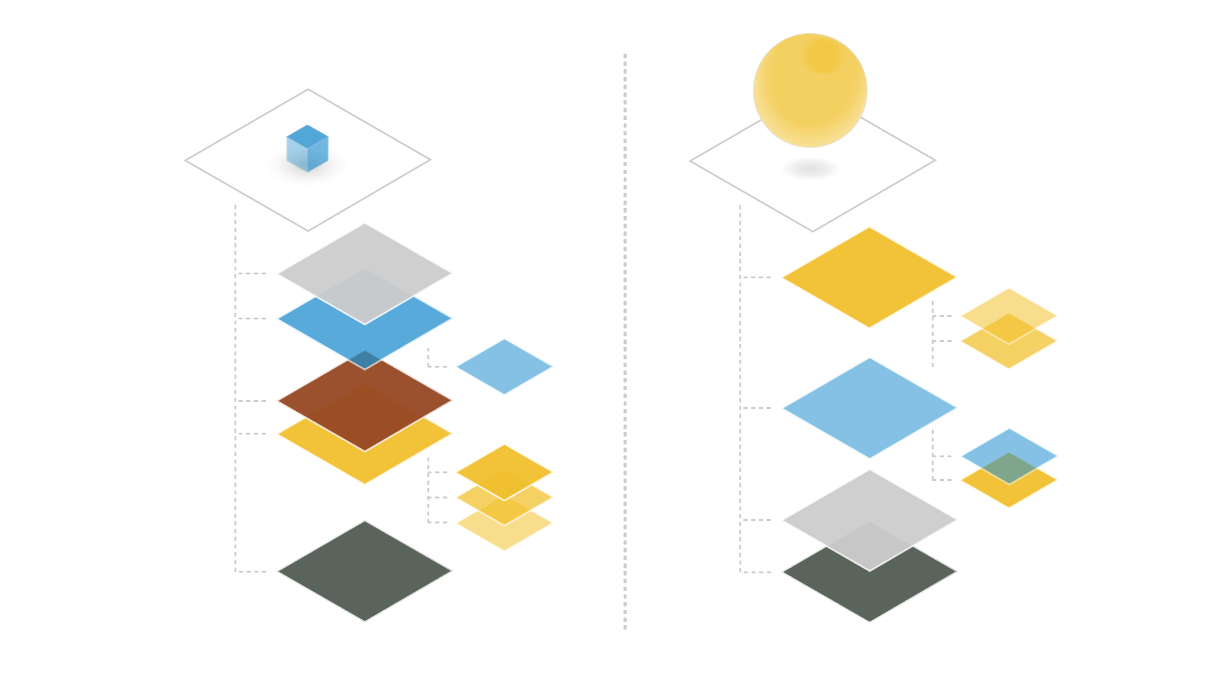
The order of the layer stack changes the composition of the scene.
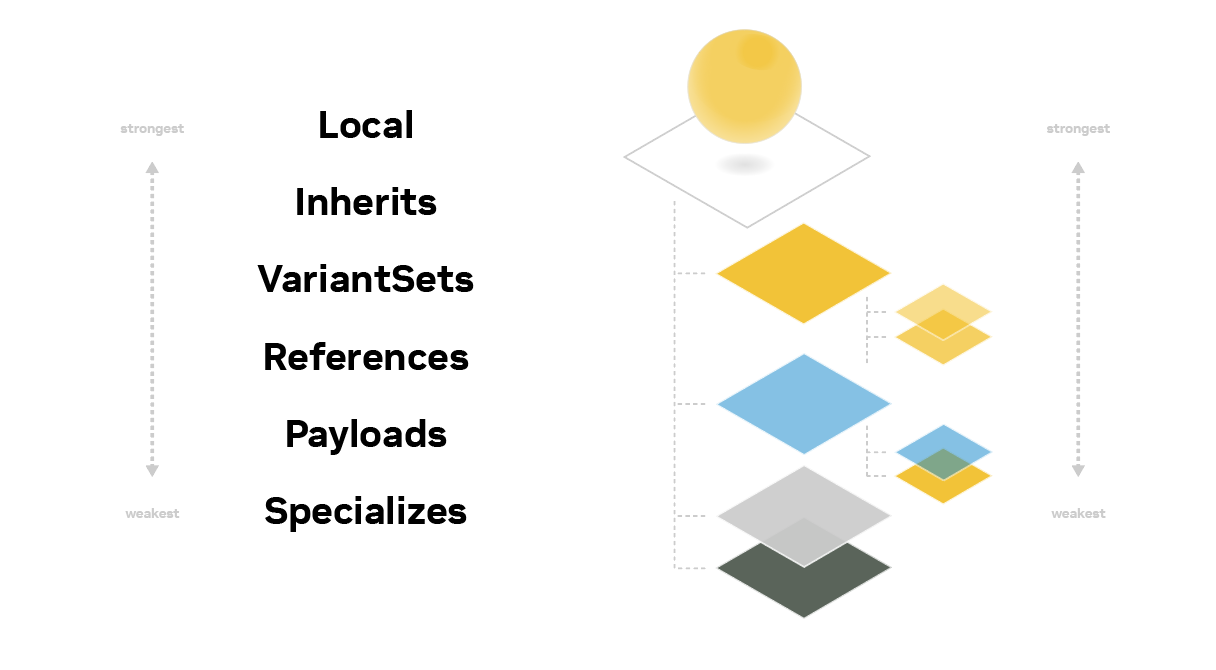
The LIVRPS acronym represents not only the different composition operations, but the order in which they are applied. This means that, when composing the opinions within a layer stack:
Local opinions are ordered first (strongest)
Opinions from inherit arcs are ordered next
Opinions from variant set arcs are ordered next
Opinions from reference arcs are ordered next
Opinions from payload arcs are ordered next
Opinions from specialize arcs are ordered last (weakest)
LIVRPS applies recursively within each composition context (layer stack)